dans cette vidéo, j’explique comment obtenir l’équation de conservation de charges électriques à partir de l’équation de maxwell-ampère et résoudre l’équatio.. La conservation de la charge électrique est un principe physique. Il exprime que la charge électrique d’un système isolé est un invariant. La charge électrique ne peut donc être qu’échangée avec un autre système mais ni créée ni annihilée. On dit qu’il s’agit d’une grandeur conservative. Ainsi, lors d’une réaction chimique, la.
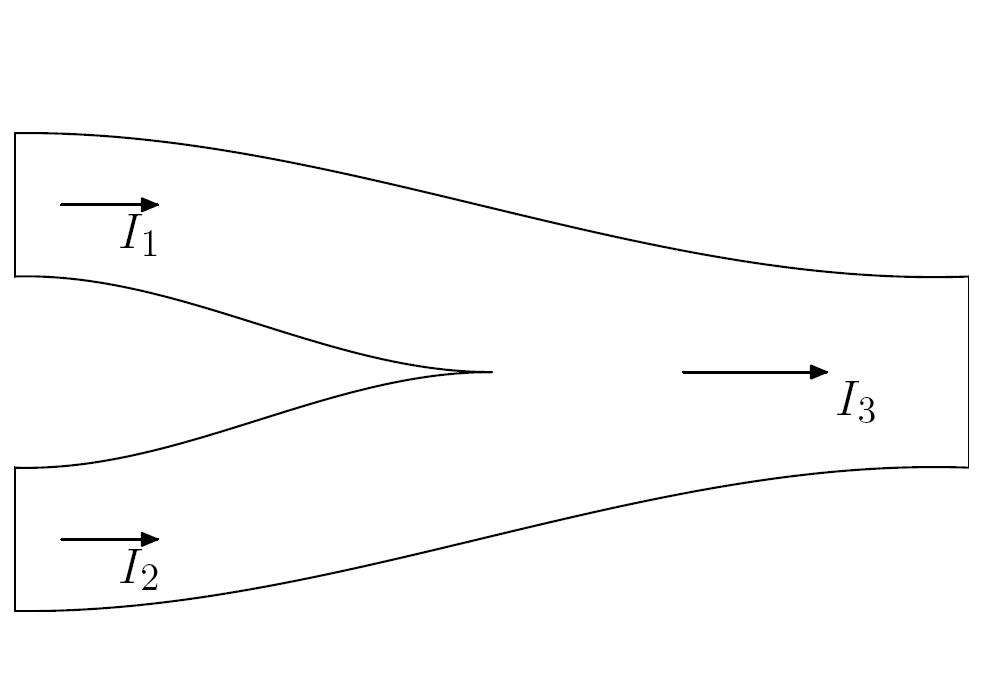
Induction et Équations de Maxwell (vide) Équation de conservation de la charge

Exercice Densité de courant et équation de conservation de charge YouTube
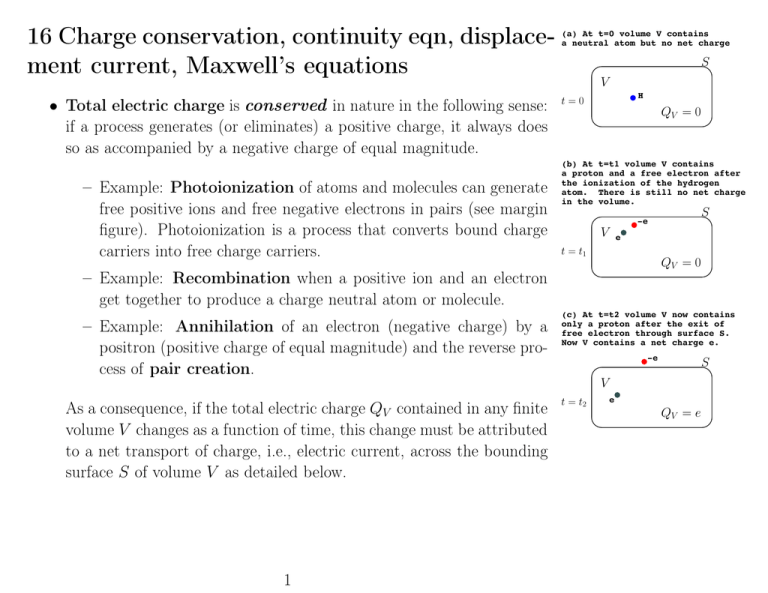
Charge conservation, continuity eqn, displacement current

PPT Maxwell’s Equations are Lorentz Invariant PowerPoint Presentation ID1414119

additivity of charge, conservation of charge (UnitI Electrostatics) YouTube

Law of Conservation of Electric Charge YouTube

PPT PowerPoint Presentation ID490986

Conservation of Charge Intro to Physics YouTube

Conservation of Charge YouTube

PPT Conservation Laws PowerPoint Presentation, free download ID183603

Principle of Charge Conservation Science In Five YouTube

Solved What equation describes conservation of charge?

La loi de la conservation de la masse et équilibrer des équations YouTube

Conservation of Charge and continuity Equation YouTube

CHAPITRE 2 lectrostatique A Principes fondamentaux B Problmatique

ÉQUATION DE CONSERVATION DE LA CHARGE YouTube
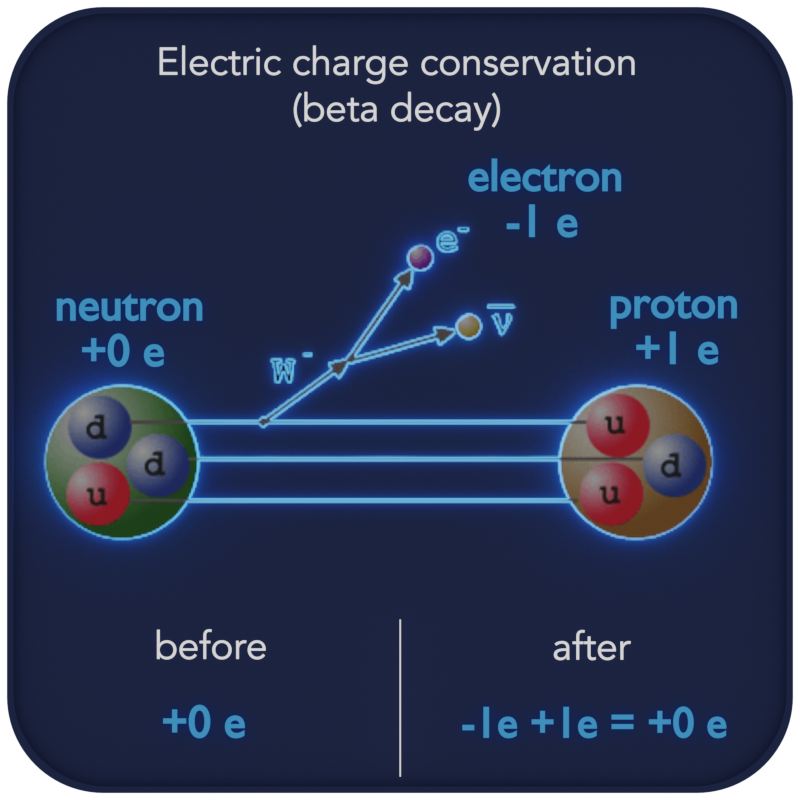
Law of Conservation of Electric Charge Statement & Example

PPT Equations de conservation PowerPoint Presentation, free download ID5630707

Equation of continuitycharge conservation equationcontinuity of chargesElectrodynamics
1. Begin with charge in a volume . We want to show that charge is locally conserved in this system. That is, any charge initially inside the volume that is found outside of the volume must have passed through the boundary. Below, is the charge density, the source of the electromagnetic field. 2.. On traduit ici de manière intégrale et locale le fait que la charge électrique se conserve, i.e. elle ne peut apparaître en un point ex nihilo, ou au contrai.




